frequency is warped and smeared; and adjacent sounds may be smeared together.
Because listeners experience auditory objects, not acoustic records like waveforms
or spectrograms, it is useful to consider the basic properties of auditory percep-
tion as they relate to speech acoustics. This chapter starts with a brief discussion
of the anatomy and function of the peripheral auditory system, then discusses
two important differences between the acoustic and the auditory representation
of sound, and concludes with a brief demonstration of the difference between
acoustic analysis and auditory analysis using a computer simulation of auditory
response. Later chapters will return to the topics introduced here as they relate to
the perception of specific classes of speech sounds.
4.1 Anatomy of the Peripheral Auditory System.
The peripheral auditory system (that part of the auditory system not in the
brain) translates acoustic signals into neural signals; and in the course of the trans-
lation, it also performs amplitude compression and a kind of Fourier analysis of
the signal.
Figure 41 illustrates the main anatomical features of the peripheral auditory
system (see Pickles, 1988). Sound waves impinge upon the outer ear, and travel
down the ear canal to the eardrum. The eardrum is a thin membrane of skin which is stretched like the head of a drum at the end of the ear canal. Like the
membrane of a microphone, the eardrum moves in response to air pressure
fluctuations.
These movements are conducted by a chain of three tiny bones in the middle
ear to the fluid-filled inner ear. There is a membrane (the basilar membrane)
that runs down the middle of the conch-shaped inner ear (the cochlea). This mem-
brane is thicker at one end than the other. The thin end, which is closest to the
bone chain, responds to high-frequency components in the acoustic signal, while
the thick end responds to low-frequency components. Each auditory nerve fiber
innervates a particular section of the basilar membrane, and thus carries infor-
mation about a specific frequency component in the acoustic signal. In this way,
the inner ear performs a kind of Fourier analysis of the acoustic signal, breaking
it down into separate frequency components.
4.2 The Auditory Sensation of Loudness.
The auditory system imposes a type of automatic volume control via amplitude
compression, and as a result, it is responsive to a remarkable range of sound inten-
sities (see Moore, 1982). For instance, the air pressure fluctuations produced by
thunder are about 100,000 times larger than those produced by a whisper (see
table 4.1).
Table 41 A comparison of the acoustic and perceptual amplitudes of some
common sounds. The amplitudes are given in absolute air pressure fluctuation
(micro-Pascals -!AN, acoustic intensity (decibels sound pressure level dB SPL)
and perceived loudness (Sones).
How the inner ear is like a piano.
For an example of what I mean by "is responsive to," consider the way in
which piano strings respond to tones. Here's the experiment: go to your
school's music department and find a practice room with a piano in it. Open
the piano, so that you can see the strings. This works best with a grand or
baby grand, but can be done with an upright. Now hold down the pedal
that lifts the felt dampers from the strings and sing a steady note very loudly.
Can you hear any of the strings vibrating after you stop singing? This experi-
n-ient usually works better if you are a trained opera singer, but an enthu-
siastic novice can also produce the effect. Because the loudest sine wave
components of the note you are singing match the natural resonant frequencies
of one or more strings in the piano, the strings can be induced to vibrate
sympathetically with the note you sing. The notion of natural resonant fre-
quency applies to the basilar membrane in the inner ear. The thick part nat-
urally vibrates sympathetically with the low-frequency components of an
incoming signal, while the thin part naturally vibrates sympathetically with
the high-frequency components.
Look at the values listed in the pressure column in the table. For most people,
a typical conversation is not subjectively ten times louder than a quiet office, even
though the magnitudes of their sound pressure fluctuations are. In general, subjective auditory impressions of loudness differences do not match sound pressure
differences. The mismatch between differences in sound pressure and loudness
has been noted for many years. For example, Stevens (1957) asked listeners to adjust
the loudness of one sound until it was twice as loud as another or, in another
task, until the first was half as loud as the second. Listeners' responses were con-
verted into a scale of subjective loudness, the units of-which are called sones. The
sone scale for intensities above 40dB SPL) can be calculated with the formula in
equation (4.1), and is plotted in figure 4.2a. (I used the abbreviations "dB" and
"SPL" in this sentence. We are on the cusp of introducing these terms formally
in this section, but for the sake of accuracy I needed to say "above 40dB SPL".
"Decibel" is abbreviated "dB'', and "sound pressure lever is abbreviated "SPL" —
further definition of these is imminent.)
The sone scale sho-ws listeners' judgments of relative loudness, scaled so that a
sound about as loud as a quiet office (2,000 Oa) has a value of 1, a sound that is
subjectively half as loud has a value of 0.5, and one that is mice as loud has a
value of 2. As is clear in the figure, the relationship benveen sound pressure and
loudness is not linear. For soft sounds, large changes in perceived loudness result
from relatively small changes in sound pressure, while for loud sounds, relatively
large pressure changes produce only small changes in perceived loudness. For
example, if peak amplitude changes from 100,0001_LPa to 200,000 .LiPa, the change
in sones is from 10.5 to 16 sones, but a change of the same pressure manimd_e
from 2,000,000 1_1Pa to 2,100,000 I_L.Pa produces less than a 2 sone change in loud-
ness from 64 to 65.9 sones).
Figure 4.2 also shows (in part b) an older relative acoustic intensity scale that
is named after Alexander Graham Bell. This unit of loudness, the bel, is too big
for most purposes, and it is more common to use tenths of a bel, or decibels
(abbreviated dE). This easily calculated scale is widely used in auditory phonetics
and psycho-acoustics, because it provides an approximation to the nonlinearity
of human loudness sensation.
As the difference between dE SPL and dB SL implies (see box on "Decibels");
perceived loudness varies as a function of frequency Figure 4.3 illustrates the rela-
tionship between subjective loudness and dB SPL. The curve in the figure repre-
sents the intensities of a set of tones that have the same subjective loudness as a
1,000 Hz tone presented at 60 dB SPL. The curve is like the settings of a graphic
equalizer on a stereo. The lever on the left side of the equalizer controls the rela-
tive amplitude of the lowest-frequency components in the music, while the lever
on the right side controls the relative amplitude of the highest frequencies. This
equal loudness contour shows that you have to amplify- the lowest and highest
frequencies if you want them to sound as loud as the middle frequencies
(whether this sounds good is another issue), so, as the figure shows, the auditory
system is most sensitive to sounds that have frequencies between 2 and 5 kHz.
Note also that sensitivity drops off quickly above 10 kHz. This was part of
my motivation for recommending a sampling rate of 22 kHz (11 kHz Nyquist
frequency) for acoustic/ phonetic analysis.
Decibels.
Although it is common to express the amplitude of a sound wave in terms
of pressure, or, once we have converted acoustic energy into electrical
energy, in volts, the decibel scale is a -way of expressing sound amplitude
that is better correlated with perceived loudness. On this scale the relative
loudness of a sound is measured in terms of sound intensity (which is pro-
portional to the square of the amplitude) on a logarithmic scale. Acoustic
intensity is the amount of acoustic power exerted by the sound wave's pres-
sure fluctuation per -unit of area. A common unit of rneasure for acoustic
intensity is Watts per square centimeter (W/ cm:).
Consider a sound with average pressure amplitude x. Because acoustic
intensity is proportional to the square of amplitude, the intensity of x rela-
tive to a reference sound with pressure amplitude r is x2/ r2, A be] is the base
10 logarithm of this power ratio: log„(x2/ r2), and a decibel is 10 times this:
10 log,o(x2/r2). This formula can be simplified to 20 loga(x/ r) = dE.
There are two common choices for the reference level r in dB measure-
ments. One is 2011Pa, the typical absolute auditory threshold (lowest audible
pressure fluctuation) of a 1,000 Hz tone. When this reference value is
used, the values are labeled dB SPL for Sound Pressure Level). The other
common choice for the reference level has a different reference pressure level
for each frequency. In this method, rather than use the absolute threshold
for a 1,000 Hz tone as the reference for all frequencies, the loudness of a
tone is measured relative to the typical absolute threshold level for a tone
at that frequency. When this method is used, the values are labeled dB SL
for Sensation Level).
In speech analysis programs, amplitude may be expressed in dB relative
to the largest amplitude value that can be taken by a sample in the digital
speech waveform, in which case the amplitude values are negative numbers;
or it may be expressed in dB relative to the smallest amplitude value that
can be represented in the digital speech waveform, in which case the ampli-
tude values are positive numbers. These choices for the reference level in
the dB calculation are used when it is not crucial to know the absolute
dB SPL value of the signal. For instance, calibration is not needed for
comparative RS or spectral amplitude measurements.
4.3 Frequency Response of the Auditory System.
As discussed in section 4.1, the auditory system performs a running Fourier anal-
ysis of incoming sounds. However, this physiological frequency analysis is not the
same as the mathematical Fourier decomposition of signals. The main difference
is that the auditory system's frequency response is not linear, just as a change of
1,000 Pa in a soft sound is not perceptually equivalent to a similar change in a
loud sound, so a change from 500 to 1,000 Hz is not perceptually equivalent to
a change from 5,000 to 5,300 Hz. This is illustrated in figure 4.4, which shows the
relationship between an auditory frequency scale called the Bark scale (wicker,
1961; Schroeder et al., 1979), and acoustic frequency in kHz. Zwicker (1975) showed
that the Bark scale is proportional to a scale of perceived pitch (the Mel scale) and
to distance along the basilar membrane. A tone with a frequency of 500 Hz has
an auditory frequency of 4.9 Bark, while a tone of 1,000 Hz is 8.5 Bark, a differ-
ence of 3.6 Bark. On the other hand, a tone of 5,000 Hz has an auditory frequency
of 19.2 Bark, while one of 5,500 Hz has an auditory frequency of 19.8 Bark, a
difference of only 0.6 Bark. The curve shown in figure 4.4 represents the fact that
the auditory system is more sensitive to frequency changes at the low end of the
audible frequency range than at the high end.
This nonlinearity in the sensation of frequency is related to the fact that the
listener's experience of the pitch of periodic sounds and of the timbre of complex
sounds is largely shaped by the physical structure of the basilar membrane.
Figure 45 illustrates the relationship between frequency and location along the
basilar membrane. As mentioned_ earlier, the basilar membrane is thin at its
base and thick at its apex; as a result, the base of the basilar membrane responds
to high-frequency sounds, and the apex to low-f•equency sounds. As figure 4.5
shows, a relatively latge portion of the basilar membrane responds to sounds below
LON Hz, whereas only a small portion responds to sounds between 12,000 and
13,000 Hz, for example. Therefore, small changes in frequency below 1,000 Hz
are more easily detected than are small changes in frequency above 12,000 Hz,
The relationship between auditory frequency and acoustic frequency shown in
figure 4.4 is due to the structure of the basilar membrane in the inner ear.
4.4 Saturation and Masking.
The sensory neurons in the inner ear and the auditory nerve that respond CO sound
are physiological machines that run on chemical supplies (charged ions of sodium
and potassium). Consequently, when they run low on supplies, or are running at
maximum capacity, they may fail to respond to sound as vigorously as usual. This
comes up a lot, actually.
For example, after a short period of silence auditory nerve cell response to a
tone is much greater than it is after the tone has been playing for a little while.
During the silent period, the neurons can fully "recharge their batteries," as they
take on charged positive ions. So when a sound moves the basilar membrane in
the cochlea, the hair cells and the neurons in the auditory nerve are ready to fire,
The duration of this period of greater sensitivity varies from neuron to neuron
but is generally short, maybe 5 to 10 ms. Interestingly, this is about the duration
of a stop release burst, and it has been suggested that the greater sensitivity of
auditory neurons after a short period of silence might increase one's perceptual
acuity for stop release burst information. This same mechanism should make it
possible to hear changing sound properties more generally, because the relevant
silence (as far as the neurons are concerned) is lack of acoustic energy at the
particular center frequency of the auditory nerve cell. So, an initial burst of
activity would tend to decrease the informativeness of steady-state sounds relative
to acoustic variation, whether there has been silence or not.
Another aspect of have sound is registered by the auditory system in tine is
the phenomenon of masking. In masking, the presence of one sound makes another,
nearby sound more difficult to hear. Masking has been called a 'line busy" effect.
The idea is that if a neuron is firing in response to one sound, and another sound
would tend to be encoded also by the firing of that neuron, then the second sound
will not be able to cause much of an increment in firing — thus the system will be
relatively insensitive to the second sound. We will discuss two types of masking
that are relevant for speech percepdon: "frequency masking' and "temporal
masking,"
Figure 4.6 illustrates frequency masking, showing the results of a test that used
a narrow band of noise (the gray band in the figure) and a series of sine wave
tones (the open circles). The masker noise, in this particular illustration, is 90 Hz
wide and centered on 410 Hz, and its loudness is 70 dB SPL, The dots indicate
how much the amplitude must be increased for a tone to be heard in the pre-
sence of the masking noise (that is, the dots plot the elevation of threshold level
for the probe tones). For example, the threshold amplitude of a tone of 100 Hz
the first dot) is not affected at all by the presence of the 410 Hz masker, but a
tone of 400 Hz has to be amplified by 50 dB to remain audible. One key aspect
of the frequency masking data shown in figure 4,6 is called the upward spread
of masking. Tones at frequencies higher than the masking noise show a greater
effect than tones below the masker. So, to hear a tone of 610 Hz (200 Hz higher
than the center of the masking noise) the tone must be amplified 38 dB higher
than its normal threshold loudness, while a tone of 210 Hz (200 Hz lower than
the center of the masking noise) needs hardly any amplification at all. This illus-
trates that low-frequency noises will tend to mask the presence of high-frequency
components.
The upward spread of masking: whence and what for?.
There are two things to say about the upward spread of masking. First, it
probably comes from the mechanics of basilar membrane vibration in the
cochlea. The pressure wave of a sine wave transmitted to the cochlea from
the bones of the middle ear travels down the hasitar membrane, building
up in amplitude (ie. displacing the membrane more and more), up to the
location of maximum response to the frequency of the sine wave (see figure
4.5), and then rapidly ceases displacing the basilar membrane. The upshot
is that the basilar membrane at the base of the cochlea, where higher fre-
quencies are registered, is stimulated by low-frequency sounds, while the
apex of the basilar membrane, where lower frequencies are registered, is not
much affected by high-frequency sounds. So, the upward spread of masking
is a physiological by-product of the mechanical operation of this little fluidfilled coil in your head,
"So what?• you may say. Well, the upward spread of masking is used
to compress sound in MP s. We mentioned audio compression before in
chapter 3 and said that raw audio can be a real bandwidth hog. The MP3
compression standard uses masking., and the upward spread of masking
in particular, to selectively leave frequency components out of compressed
audio. Those bits in the high-frequency Lail in figure 4,6, that you wouldn't
be able to hear anyway? Goner have space by simply leaving out the inaudible bits.
The second type of masking is temporal masking. What happens here is that
sounds that come in a sequence may obscure each other. For example, a short,
soft sound may be perfectly audible by itself, but can be completely obscured if
it closely follows a much louder sound at the same frequency There are a lot of
parameters to this "forward masking" phenomenon. In ranges that could affect
speech perception, we would note that the masking noise must be greater than
40 dB SPL and the frequency of the masked sound must match (or be a frequency
subset of she masker. The masking effect drops off very quickly and is of almost
no practical significance after about 25 ins. In speech, we may see a slight effect
of forward masking at vowel offsets (rowels being the loudest sounds in speech).
Backward masking, where the audibility of a soft sound is reduced by a later-
occurring loud sound, is even less relevant for speech perception, though it is
an interesting puzzle how something could reach back in Lime and affect your
perception of a sound. It isn't really magic, though; just strong signals traveling
through the nervous system more quickly than weak ones.
4.5 Auditory Representations.
In practical terms what all this means is that when we calculate an acoustic power
spectrum of a speech sound, the frequency and loudness scales of the analyzing
device (for instance, a computer or a spectrograph) are not the same as the audi-
tory system's frequency and loudness scales. Consequently, acoustic analyses of
speech sounds may not match the listener's experience. The resulting mismatch
is especially dramatic for sounds like some stop release bursts and fricatives that
have a lot of high-frequency energy and/ or sudden amplitude changes. One way
to avoid this mismatch between acoustic analysis and the listener's experience
is to implement a functional model of the auditory system. Some examples of
the use of auditory models in speech analysis are Liljencrants and Lindblom (1972),
Bladon and Lindblom (1981), Johnson (1939), Lyons (1982), Patterson (1976), Moore
and Glaslierg (1983), and Seneff (1988). Figure 4.7 shows the difference between
the auditory and acoustic spectra of a complex wave composed of a 500 Hz and
a 1,500 Hz sine wave component. The vertical axis is amplitude in dB, and the
horizontal axis shows frequency in Hz, marked on the bottom of the graph, and
Bark, marked on the top of the graph. I made this auditory spectrum, and others
shown in later figures, with a computer program (Johnson, 1939) that mimics the
frequency response characteristics shown in figure 4.4 and the equal loudness con-
tour shown in figure 4,3. Notice that because the acoustic and auditory frequency
scales are different, the peaks are located at different places in the two represen-
tations, even though both spectra cover the frequency range from fl to 10,000 Hz,
Almost half of the auditory frequency scale covers frequencies below 1,500 Hz,
while this same range covers less than two-tenths of the acoustic display So, low-
frequency components tend to dominate the auditory spectrum. Notice too that
in the auditory spectrum there is some frequency smearing that causes the peak
at 11 Bark (1,500 Hz) to be somewhat broader than that at 5 Bark (500 Hz). This
spectral-smearing effect increases as frequency increases.
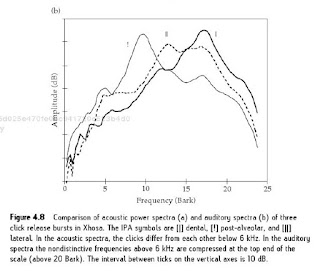
Figure 4.3 shows an example of the difference between acoustic and auditory
spectra of speech. The acoustic spectra of the release bursts of the clicks in Xhosa
are shown in (a), while (b) shows the corresponding auditory spectra. Like figure 4.7,
this figure shows several differences between acoustic and auditory spectra. First,
the region between 6 and 10 kHz (20-4 Bark in the auditory spectra), in which
the clicks do not differ very much, is not very prominent in the auditory spectra.
In the acoustic spectra this insignificant portion takes up two-fifths of the frequency
scale, while it takes up only one-fifth of the auditory frequency scale. This serves
to visually; and presumably auditorily, enhance the differences between the
spectra. Second, the auditory spectra show many fewer local peaks than do
the acoustic spectra. In this regard it should, be noted that the acoustic spectra
shown in figure 4.8 were calculated using LPC analysis to smooth them; the FFT
spectra which were input CO the auditory model were much more comphcated
than these smooth LPG spectra. The smoothing evident in the auditory spectra,
on the other hand, is due to the increased bandwidths of the auditory filters at
high frequencies.
Auditory models are interesting, because they offer a way of looking at the speech
signal from the point of view of the listener. The usefulness of auditory models
in phonetics depends on the accuracy of the particular simulation of the peri-
pheral auditory system. Therefore, the illustrations in this book were produced by
models that implement only well-known, and extensively studied, nonlinearities
in auditory loudness and frequency response, and avoid areas of knowledge that
are less well understood for complicated signals like speech.
These rather conservative auditory representations suggest that acoustic ana-
lyses give only a rough approximation to the auditory representations that
listeners use in identifying speech sounds.
Recall from chapter 3 that digital spectrograms are produced by encoding
spectral amplitude in a series of FFT spectra as shades of gray in the spectrogram.
This same method of presentation can also be used to produce auditory spec-
trograms from sequences of auditory spectra. Figure 4.9 shows an acoustic
spectrogram and an auditory spectrogram of the Cantonese word ikal "chicken (see
figure 3.20). To produce this figure, I used a publicly available auditory model (Lyons'
cochlear model (Lyons, 1932; Marley, 1988), which can be found at: http:
linguistics,berkeleyedulphonlablresourcesl ). The au di to ry spectrogram , which
is also called a cochleagram, combines features of auditory spectra and spectro-
grams. As in a spectrogram, the simulated auditory response is represented with
spectral amplitude plotted as shades of gray, with time on the horizontal axis
and frequency on the vertical axis. Note that although the same frequency range
(0-11 kHz) is covered in both displays, the movements of the lowest concentra-
tions of spectral energy in the vowel are much more visually pronounced in the
cochleagram because of the auditory frequency scale.
Recommended Reading
Bladon„ A. and Lindblom, B. (1981) Modeling the judgement of vowel quality differences. Journal of the Acousticai Society of America, 69, 1414-22. Using an auditory model to predict vovi,rel perception results.
Brody 1* livi, (1946) Three Unpublished Drawings of the Anatomy of the Human Ear, Philadelphia: Saunders. The source of figure 4.1.
Johnson, K. (1989) Contrast and normalization in vowel perception. Journal of Phonetics, 18, 229-54. Using an auditory model to predict vowel perception results.
Liliencrants, J. and Lindblom, Bjorn (1972) Numerical simulation of vowel quality systems: The role of perceptual contrast. Language, 48, 839-62. Using an auditory model to predict cross-linguistic patterns in vowel inventories,
Lyons, R. F. (1982) A computational model of filtering, detection and compression in the cochlea. Proceedings of the IEEE international Conference on Acoustics, Speech and Signal Processivg, 1282-5. A simulation of the transduction of acoustic signals into auditory nerve signals. Slaney's (1988) implementation is used in this book to produce "cochlea-
1'2
grams.
Moore, B. C. J. (1982) An introduction to the Psychology of Hearing, 2nd edn., New York: Academic Press. A comprehensive introduction to the behavioral m.easurement of human hearing ab ilit — auditory psychophysics.
Moore, B. C. J. and Glasberg, B. R. (1983) Suggested formulae for calculating auditory-filter bandwidths and excitation patterns. puma! of the Acoustical Society of America, 74, 750-3. Description of the equivalent rectangular bandwidth (ER.B) auditory frequency scale and showing how to calculate simulated auditory spectra. from this information.
Patterson, R. D. (1976) Auditory filter shapes derived from noise stimuli. JoHniai of the Acoustical Society of America, 59, 640-54, Showing how to calculate simulated auditory spectra using an auditory filter-bank.
Pickles, J. O. (1988) An Introduction to the Pitysioiogy offlearing, 2nd ecln., New York: Academic Press. An authoritative and fascinating introduction to the physics and chemistry of hearing, with a good review of auditory psychophysics as well.
Schroeder, M. R., Atal, B. S., and Hall, J. L. (1979) Objective measure of certain speech signal degradations based on masking properties of human auditory perception. In B. Lindblom and S. hman (eds.), Frolifiers ofSpeech Commi.inication. Research, London:. Academic Press, 217-29. Measurement and use of the Bark frequency scale.
Seneff, 5, (1988) A joint synchronytmean-rate model of auditory speech processing. Journal of Phonetics, 16, 55-76.
Sian ey, M. (1988) Lyons' cochlear model. Apple Technical Report, 13. Apple Corporate Library., Cupertino, A. A publicly distributed implementation of Richard Lyons' (1982) simulation of hearing.
Stevens., S. S. (1957) Concerning the form of the loudness function...loin-nal of the. Acoustica Society of America., 29, 603-6. An example of classic 1950s-style auditory psych ophysics in Avhich the sone scale was first described.
Zwicker, E.. (1961) Subdivision of the audible frequency range into critical bands (Frequen.zgruppen). Journcd of tile Acoustical Society ofAmerica 33, 248. An early descrip-tion of the Bark scale of auditory critical frequency bands.
Zwicker, E. (1975) Scaling. In W. D. Keidel and NV. D. Neff (eds.), Auditory System: Physioiogy (CNS), behavioral studies, psycho ottstics, Berlin: Springer-Verlag. An overview of various frequency and loudness scales that were found in auditory psychophysics research.













No hay comentarios.:
Publicar un comentario